P.A.M. Dirac was an English theoretical physicist famous for his relativistic theory of quantum mechanics which he developed in the 1920s.  In the course of that work he investigated the concept of orientation, that is, the position of an object with regard only to how it is turned or tilted.

Consider an object that can rotate in any way about a fixed point but cannot move otherwise. If the object is flat and confined to a plane you can describe its position with just one number. First designate one position of the object as the reference position, then any other position can be obtained from this reference position by rotating about the fixed point. The angle of rotation can be constrained to be less than 360° and greater than or equal to zero, and that would cover all possible positions.

If the object is a solid in space the problem is more complicated. One solution is analogous to that in the plane and uses the following fact, discovered in the 18th century by the Swiss mathematician Leonhard Euler: the general displacement of a rigid body with one point fixed can be obtained by one rotation about some axis passing through the fixed point. This isn’t obvious, but being true it gives a simple way to specify the position of the object. Again designate one position of the object as the reference position. Since any other position can be obtained by starting from the reference position and rotating about an axis, represent the position by that direction (the axis of rotation) together with the angle (how much to rotate).

However the many possible positions of an object are described, they could be considered all at once as a sort of “space” itself – in other dimensions – each “point” of this space representing one position. A movement of the object (about its fixed point) from one position to another would be represented in this “position space” by a path from one point to another.

The position space is connected in a peculiar manner and Dirac thought of a simple way to illustrate it. We go into more detail in the succeeding sections. Since the position space is the same for any object whatever its shape or size, we will be specific by making the object a sphere and the fixed point its center. [0]

Suppose a sphere’s center is fixed but the sphere is otherwise free to turn in any way. How can we distinguish and label each of the positions the sphere could occupy?

First consider the sphere in some arbitrary position. As we claimed before, the sphere at any other position can be thought of as the result of rotating  the sphere starting from that first position. Call the first position the reference  position.

It isn’t obvious that any position can be reached from the reference position by just one rotation, that is, directly turned about one axis with no wobbling. We won’t prove it hear but in fact, given any two positions of the sphere there always exists a rotation, about a certain axis through a certain angle, that will take the sphere from the one position to the other. Furthermore, the angle can be required to be between 0 and 180° inclusive. This rotation is unique if the angle is not 0 or 180°, that is, if it is strictly within the range 0 to 180°.

This axis-angle can be represented by a vector: an arrow in the line of the axis, with its length equal to the rotation angle (using some arbitrary factor to convert angle units into distance units, say 1 for 1 radian). [1]  The vector is unique if we agree to ignore the difference between two vectors in opposite directions when the angle of rotation (the length of the vector) is 180°,  because rotating the sphere through 180° about either vector gives the same final position. [2]

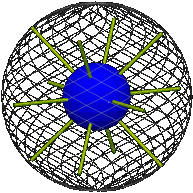
In this way we construct a vector that represents the position of the sphere; we can recover the rotation given the vector. Now regard this vector as the position  vector of a point  in Euclidean space. [3]  The point lies in what we shall call the position space  of the sphere. [4]  It is a ball of radius  π  radians, but with the proviso that diametric points on its surface are thought of as interchangable – because they represent one and the same position of the sphere. [5]  The center of this ball represents the reference sphere. Any other point represents the position obtained by rotating the reference sphere about the point’s position vector, through an angle equal to its length. [6]

Note that the radius of the sphere does not enter into what we have been calling its position. We can compare the positions of large and small spheres using the same  position space, given that their positions are the same when both are in their reference positions. In what follows we will use “sphere position” in this sense of “sphere orientation” and disregard the sphere’s radius.

We will call the reference position zero.

After setting up a rectangular coordinate system for the natural space of the sphere, the same coordinate system can be used in the position space even though that space is an abstract space. Position space was obtained by regarding the rotation vectors in the sphere’s natural space as position vectors of points in the abstract space. We can use the same coordinate system in both spaces. (Say the x-axis goes to the right, the y-axis into the screen, the z-axis up.)

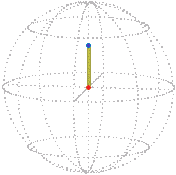
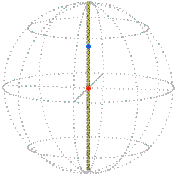
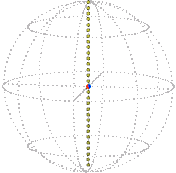
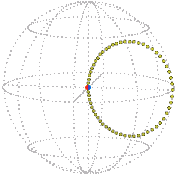
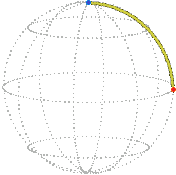
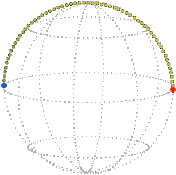
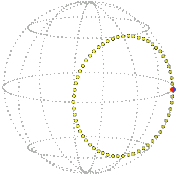
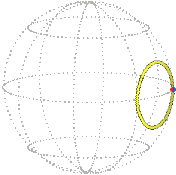
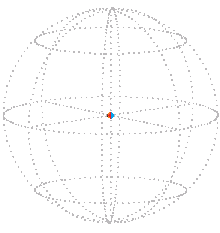
For example, a simple rotation about the vertical by  π / 2  (90°) that starts from the reference position (zero) is represented in position space by a radial line segment. The orange dot is at the starting position, the blue dot is at the ending position:

Position space.

There is another way to record the movement of a sphere, within its natural space rather than an abstract space. First consider a similar problem. Suppose we wanted to record the motion of a square sliding about in the plane. If we were to move that plane perpendicular to itself at a steady speed, the square would sweep out a solid. This timeless solid would be a record of all the positions the square had occupied during the course of its travel in the plane. The time  t  in the plane becomes the distance  t  perpendicular to the plane.

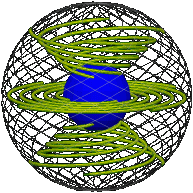
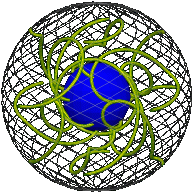
We have a sphere rather than a flat square, but a similar idea works: shrink  the sphere at a constant rate. The resulting solid records the motion of the sphere. (The well known model of the tesseract or hypercube, the four-dimensional cube, uses a similar idea. Our solid is like the lateral surface of a four dimensional cylinder with the outer and inner spheres as its two end caps.) The outer sphere represents the sphere at its starting position, the inner sphere represents the sphere at its final position.

Real space.
	·······    t  =  0   rim   ·······    t  =  1   core

Later we will be considering “motions of the motion,” so think of the solid as made of elastic material attached to the inside surface of the rigid rim and to the outside surface of the rigid core.

Imagine the elastic divided into innumerable concentric spheres between the rim and core. We shall call any such intermediate sphere between the rim and core an intersphere. The collection of interspheres records the motion of a sphere. Each sphere at a different time is an intersphere. The reference position (zero) is the rim and the final position is the core.

Now we have two ways of representing the motion of a sphere: either as a path in position space starting at zero, or as a particular position of the elastic between rim and core. Canceling out the mediating idea of the moving sphere leads to the following observation:

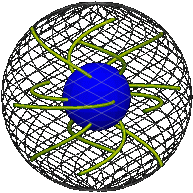
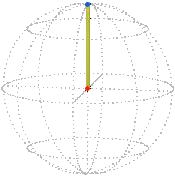
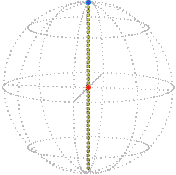
The simple path in position space illustrated in the previous section translates into a position of the elastic illustrated below at right, where we show only a few “ropes” within the elastic. The point, depicted as a dot, in position space representing the rim is colored orange (always at the center) and that for the ball blue.

Position space.	Real space.

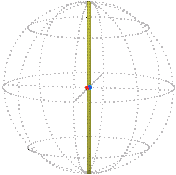
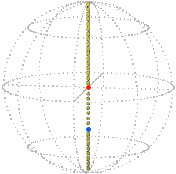
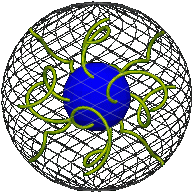
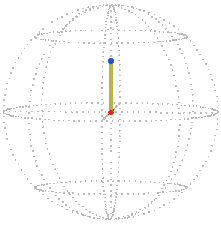
There is a special position of the elastic whose corresponding path we will need to know, namely its initial position when the elastic is untwisted. The path for this begins at zero and stays there because all the interspheres, including the core, are in the same position as the rim. The following shows the path in position space (the dot is colored half orange and half blue) and the corresponding position of the elastic indicated by a few ropes within it.

Position space.	Real space.

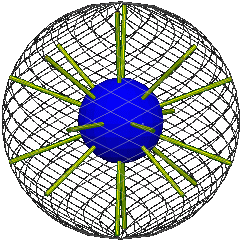The “continuous elastic material” can be represented by a function on the space between the rim and core. However, colloquial language handles motion more easily than mathematical notation. The problem with mathematical notation is that in order for a point to retain its identity in another position, one must resort to a function. [8]

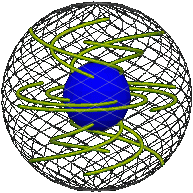
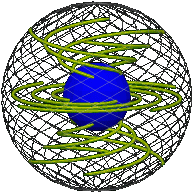
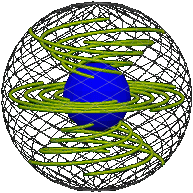
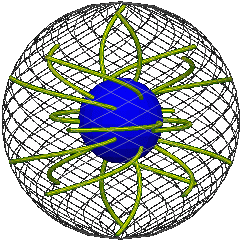
As the motion progresses the imaginary interspheres slide against one another, shearing and twisting at different points in between, while each remains rigid and within itself.

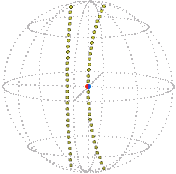
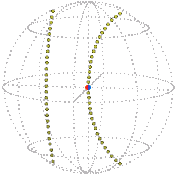
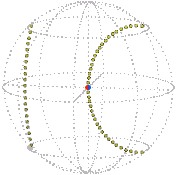
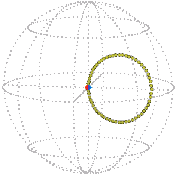
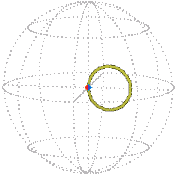
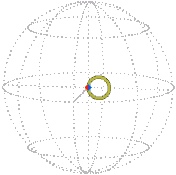
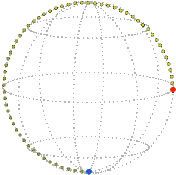
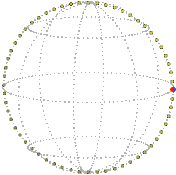
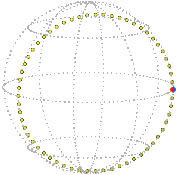
Here is the core turning about exactly once about the vertical axis, the elastic passively following, as represented in real space and position space (snapshot each quarter turn). Imagine a sphere shrinking as it turns, each circle on it tracing out a rope:

Now suppose the core turns about once more, twice in all, the elastic passively wrapping around it as before. As the core performs this 720° turn its point in position space starts at zero and moves up the vertical diameter twice. The remainder of the elastic is represented by the straight line segment from the center to that point. Let the time  s  go from 0 to 1 over the course of the two turns, so the above illustrates  s = 0 to .5.  In the following illustration the path in position space is indicated by 60 dots along its length to better reveal its motion as  s = .5 to 1.  As before the rim dot is colored orange, the core dot blue. (When the dots coincide at the center, it is half orange and half blue.)

The final position of the elastic wraps about the core twice, and the corresponding path in position space covers the vertical diameter twice. Unlike the final path of the 360° turn in the previous example, which covers the vertical diameter once, the final path above can be shrunk to zero, that is, to the path that remains at zero, by taking advantage of the peculiar connectivity of position space.  From time  s = 1 to 2:

From  s = 1 to 2  the above path motion represents a motion of the elastic from twisted twice around to straight. In other words, by using the above as a guide, the elastic – or any ropes, strings, threads or whatever into which it is divided – can be untwisted and untangled back to the original position while the core remains fixed after two turns.

Note that we were able to choose paths that lie in a plane. You could take a cross-section of the “pi ball” to obtain a “pi disk” containing the entire path motion.

To repeat, let  s  be the time, starting at  s = 0  when the core starts to move. In the elastic motion we have in mind, the core turns at a constant rate from  s = 0 to 1,  the elastic passively following, then the core stops and stays still from  s = 1 to 2  as the elastic moves back to where it was when it started.

Since we are determining a particular motion of the elastic,  s  also labels the position of the elastic, that is,  s  can be considered a parameter that specifies a path in the “sequence” of paths in the above figure.

For each  s,  then, we have a path. Let  the variable  t  indicate the point that is  t  of the way along the path, which path is the position of the corresponding intersphere  t  inwards from the rim towards the core.  t  runs from 0 (rim) to 1 (core).

Then finding the elastic is just a problem in analytic geometry. For each time  s  we have a path in position space  p (t).  Convert each point on the path given by  t  to an axis and angle, then use the rotation formula in footnote 6 above to find the coordinates of any point on the intersphere t of the way in from the rim.  Thus for any  s,  we know the position of the entire elastic  t = 0 to 1.

Dirac invented the elastic to illustrate paths in position space. We have seen how position space can be used to describe exactly how the elastic moves.

That you can somehow or other untwist one rope (after two turns, not after one) might be expected. What is surprising is that you can untwist any number of ropes simultaneously.

What at first glance appears to be a complicated and eminently three dimensional problem, keeping ropes untangled while attached to a whirling ball, becomes a fairly simple two dimensional problem by using the right mental tools.

If you rotate the scissors once around then hold them still, try as you might you cannot manipulate the strings to remove the twist (though you can twist them in the other direction or make them more twisted). But if instead you rotate the scissors twice around before holding them still, you can remove the twist.

Of course the trick works with any object besides scissors and with any number of strings. It’s not so obvious, though, that it works if the strings can be in any direction tied to something that entirely surrounds the object, as in the rim-core exposition above.)

In general – that is, always – an odd number of rotations produces a twist that cannot be undone whereas with an even number it can.

Then there is the waiter’s  plate trick.

Dale A. Adams, of Tucson, Arizona, discovered how, and designed and built a machine to do it. His machine moves a rope – or an electric cable, flexible tube, reflected light beam, etc. – in such a way around a turntable, and at the same time supports and drives the turntable. Today his invention is used in apheresis and other centrifuges, and a twister version to spin fiber into thread. (The motion of the twister version goes back to ancient times but his gearwork was original.)

See  U.S. patent 3,586,413  “Apparatus for Providing Energy Communication Between a Moving and a Stationary Terminal” filed March 25, 1969, issued June 22, 1971.

In the axis-angle representation consider any point  (θ a₁, θ a₂, θ a₃)  where  (a₁, a₂, a₃)  is a unit axis vector and  θ  an angle of rotation. The_. corresponding point-pair on the Euler parameter sphere is  ± (c, s a₁, s a₂, s a₃)  where  c = cos (θ/2)  and  s = sin (θ/2).  Diametrically opposite points represent the same position. [9]

The position of the stationary rim is represented by  ± (1, 0, 0, 0)  in Euler parameters. A position of the elastic is represented by a path starting from this point. If one of the last three of the four coordinates is zero all along the path, you can take a cross-section of the sphere in four dimensions to obtain an ordinary sphere in three in three dimensions – a “great sphere” analogous to a great circle – that contains the entire path. (In the axis-angle representation the same path will lie in a plane, as described in the previous section.)

In the particular moving and untangling of the elastic already described, the motion is “planar,” that is, the axis-angle path lies in a plane and the Euler parameter path lies in an ordinary sphere. If we arbitrarily assign the three non-zero Euler parameters to three axes of ordinary space we obtain the following path motion. (In the pictures below, the reference point (1, 0, 0, 0) → (1, 0, 0) is the extreme right point of the sphere.)

Euler parameters are related to quaternions, a number system discovered by William Rowan Hamilton in the 19th century. Unit quaternions are Euler parameters with an algebraic structure, that is, there is a rule for multiplying them together. Though enlightening in other respects the algebra isn’t needed in the above computation.

The Euler sphere is the best representation of position space in that, unlike with axis-angle or any other method, it gives equal weight to all positions. If you take any two points of the Euler sphere and rotate them to another place (that is, rotate the real sphere from each position and consider the two new position points), the distance between them remains unchanged.