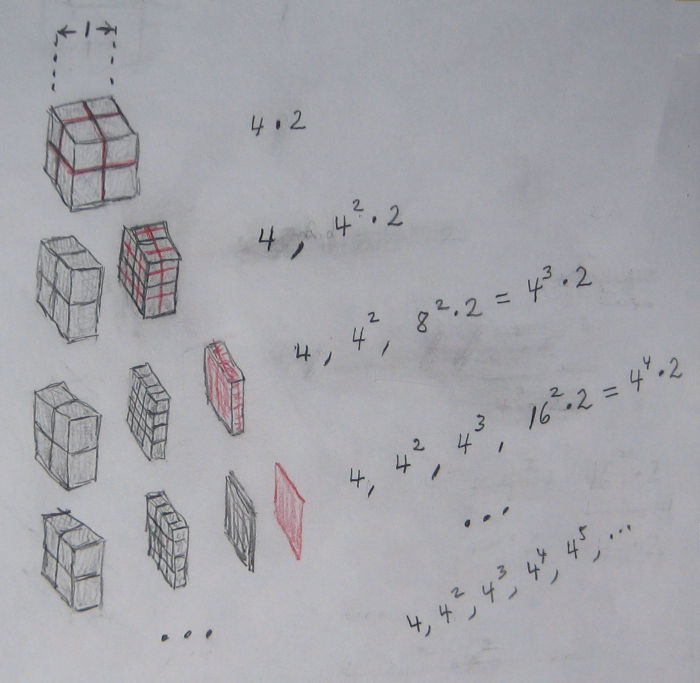<< Algorithms

A New Look at Torricelli’s Trumpet

To make a solid dissolve in a liquid more quickly you can first crush the solid into small particles.  Because the solid dissolves at its exposed surfaces, increasing the exposed surface area by breaking it up into smaller pieces makes more of it dissolve at the same time.

This suggests an elementary way to create a solid whose volume is limited yet whose surface area is unlimited, and for which computing those two quantities is easy – a sort of rough and ready version of Torricelli’s Trumpet.

Torricelli’s Trumpet is the solid formed by revolving the graph of  1 / x  for  x ≥ 1  about the  x-axis.  The volume enclosed by Torricelli’s Trumpet is finite, namely  π,  but its surface area is infinite, that is, it becomes as large as you please if you let the right end extend far enough.  But to do those computations requires calculus or at least Cavalieri’s method of indivisibles. [*]

Our trumpet is much simpler, if not as elegant-looking, as Torricelli’s.

First imagine a solid cube one inch wide.  Its volume is one cubic inch, its surface area six square inches.  Slice the cube in half three times through three perpendicular planes, making 8 smaller cubes  1/2  inch wide.  Then for just the  4  cubes to the right, slice each in half three ways as before, making  4 · 4 = 16  smaller cubes  1/4  inch wide.  Again choose the right half of those cubes and slice, etc.  In the diagram below the numbers on the right count the small cubes on the left.  (You can  right-click / click “View Image”  to enlarge the diagram.)
Do this ad infinitum, obtaining:
4   cubes  1/2  wide
42 cubes  1/22 wide
43 cubes  1/23 wide
...

Naturally at each step the total volume of all the cubes equals the volume of the original cube, that is, one cubic inch.

Now string out the cubes in a line from largest to smaller and smaller, each cube touching the ones to its left and right.  Then add a single cube of unit width at the left (which can be thought of as  40 cubes  1/20 wide).  Finally, hollow out the whole business, including the left unit square, leaving only the surface.  The result is a rough sort of trumpet:
It’s volume is two.  The lengths of the segments grow exponentially while their widths decrease exponentially.  As the sequence continues ad infinitum the length of the trumpet increases likewise:
1 ·1  +  4 ·1/2  +  16·1/4  +  64·1/8  +  ...
=  1  +  2  +  4  +  8  +  ...
=  ∞

Its lateral surface area is four times [**]
1·12  +  4·(1/2)2  +  16·(1/4)2  +  64·(1/8)2  +  ...
=  1  +  1  +  1  +  1  + ...
=  ∞

Thus we have a solid whose volume is two and whose surface area is infinite. [***]

The sequence of cubes approximates Torricelli’s Trumpet.  Place the sequence of cubes along the  x-axis  with the left unit cube just to the right of  x = 1.  The size of the cube at the beginning of each segment equals  1 / x:
     x     cube width
1       1
2  to  4       1 / 2
4  to  8       1 / 4
8  to  16       1 / 8
16  to  32       1 /1 6
    ···         ···


*  Evangelista Torricelli (1608 - 1647).  Torricelli’s Trumpet is also known as Gabriel’s Horn;  Torricielli himself called it the hyperbolicum acutum.  Cavalieri’s method of indivisibles in particular cases goes back to Archimedes.   The picture of Torricelli’s Trumpet, necessarily abridged, is due to “RokerHRO” using Persistence of Vision Raytracer (POV-Ray), and which he placed in the public domain.

Torricielli calculated the volume as follows.  The Trumpet surface is generated by rotating the graph of  y = 1 / x  about the  x-axis.  For each  y  between  0 and 1  consider the line segment parallel to the  x-axis  from the  y-axis  to the graph.  Rotating it about the  x-axis  generates a cylinder of radius  y  and length  x , which equals  1 / y.  Its left circular cap is at  x = 0  and its right circular cap is at  x = 1 / y  on the Trumpet.  Its circumference is  2 π x , so its area, which is its circumference times its length, is  2 π  independent of  y.  That independence makes the rest of the calculation easy.  Torricelli “integrated” all the cylinders from  y = 0 to 1 , which together fill the Trumpet plus cylinder outside it, using a novel application of Cavalieri’s method of indivisibles to curved surfaces.  However we can just integrate the constant from  0 to 1  to get the volume:  2 π.  Since that includes the left end of the solid cylinder outside the Trumpet from  x = 0 to 1  whose volume is  π,  we subtract that to obtain the volume of the Trumpet:  π.

I don’t know how Torricelli concluded that the surface area was infinite, but one way to see it is to inscribe cylinders at unit intervals along the x-axis.  Individually their surface area is less than the surface area of the corresponding part of the Trumpet surrounding the cylinder.  As you go to the right,  x = 1, 2, 3, ...,  the lateral area of the cylinder is a constant factor times  1 / x.  Thus the total lateral area of the cylinders is a factor times the sum of the harmonic series  1/2 + 1/3 + 1/4 + ...  which is easily seen to diverge.  (Group the first number, the next two, the next four, the next eight, etc.  The sum of each group exceeds – or equals in the case of the first group – the last member times the number of members, that is, 1/2.  Thus the sum exceeds  1/2 + 1/2 + 1/2 + ...  which diverges.)

For that matter, one could show that the volume of the Trumpet is finite by likewise superscribing it with cylinders. Each cylinder volume exceeds the corresponding Trumpet part volume.  The volume of a cylinder beginning at  x  is a constant factor times  1 / x2.  Thus the total volume of the cylinders is that factor times the sum of the series  1 + 1/22 + 1/32 + ...,  which converges, though the proof is sophisticated.

**  By lateral surface we mean the surface parallel to the xy or xz planes and neglecting surface perpendicular to the x-axis.  Even were we to include the latter it wouldn’t matter because it turns out the former is infinite.  However it is easy to figure out what it is.  Imagine looking at the trumpet along the x axis from +∞. You would see only the area perpendicular to the x axis and its total is the same as the facing side of the first cube of width 1, the sillouette of the trumpet.  Thus the non-lateral surface area is 1.

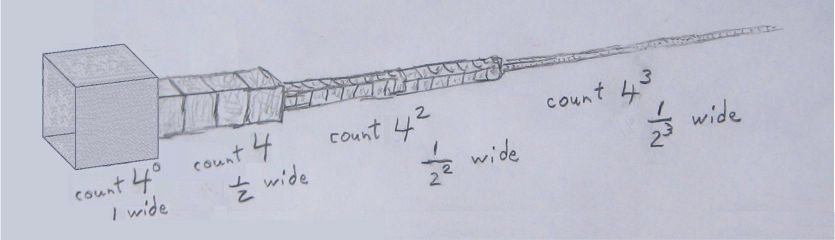
***  Number the segments by  0, 1, 2, 3, ...  where
0  indicates the single cube segment of width 1,
1  indicates the four cube segment of width 1/2,
2  the sixteen cube segment of width 1/4,
etc.
For segment  N:
number of cubes  C  =  4N
width  W  =  (1/2)N
length  L  =  W·C  =  2N
area of one of the four lateral sides  A  =  L·W  =  1
volume  V  =  W2·L  =  1/2N
Thus as N increases, the volume of the individual segments decreases exponentially while the surface area remains constant.