<< Algorithms

The Turn Sphere
- a theorem of Biedenharn and Louck -

There is another way to represent a rotation – and thus an orientation given a reference orientation – besides as a point of the axis-angle ball or of the quaternion unit sphere. [*]  It is as a “curved arrow” on the unit sphere, that is, a directed arc of a great circle. Such a curved arrow represents rotating about the center of the sphere in the direction of the arrow through an angle indicated by its length. The sphere, like the axis-angle ball and unlike the quaternion unit sphere, resides in ordinary three dimensional space.


The plane of the curved arrow’s great circle is perpendicular to the arrow in the axis-angle space. No right hand rule is needed to determine the rotation’s direction.


From the point of view of the sphere (had it eyes) the curved arrow is straight: its lateral curvature is zero.

We can slide a curved arrow anywhere along its great circle, its arc length remaining constant, and it will specify the same rotation. In mathematical jargon, one curved arrow determines an “equivalence class” of curved arrows on its great circle. We call such an equivalence class a Turn, in effect a rotation but with a graphical emphasis. At times we may just refer to a curved arrow and leave the equivalence class it represents, the Turn, understood. We call the unit sphere, with its freight of potential curved arrows, the Turn Sphere.

Within the axis-angle ball there is a point for every rotation and so, by Euler’s theorem, collectively the points cover all orientations. Since the correspondence is continuous, orientation space has the same dimension as the ball, that is, three. On the Turn Sphere there are ordered pairs of points (the head and tail of a curved arrow) that determines any rotation. At first glance this space of point-pairs has four dimensions (two times two) but the fact that the pair of points can slide along a great circle (one dimension) and represent the same rotation reduces that by one. Thus the third orientation space likewise has three dimensions, as it must.

In the axis-angle ball the point at the center represents no rotation, or the null rotation (the reference orientation). On the Turn Sphere any curved arrow of zero length – an overlapping pair of points, anywhere on the sphere – represents the null rotation. All null Turns are equivalent, or rather, there is only one null Turn.

A curved arrow on the Turn Sphere looks similar to a vector in the plane drawn as a directed line segment or straight arrow. The sphere arrow specifies a rotation, the plane arrow a translation. Focus on the plane for a moment. A plane arrow’s direction is the direction of the translation and its length indicates how far to move.


The arrow can be slid along the line of which it is a part and still represent the same translation. (It can be slid outside its line as well, just so its direction remains the same but in what follows we shall avoid using that fact. Its analogue on the sphere doesn’t hold because a direction on the sphere after “parallel transport” depends on the path over which it is moved.)

Given two translations, the result of performing one then the other is equivalent to another, single, translation. We can determine its arrow by adding the arrows of the given translations using the following geometric construction. We consider only the case when the lines of the two arrows intersect. (Parallel lines have no analogue on the sphere – all great circles intersect.) Slide the first arrow along its line so its head meets the intersection of the two lines. Slide the second arrow so its tail meets the first arrow’s head. Then the arrow from the first’s tail to the second’s head is the sum of the two given arrows.

   

To repeat, the composition of two translations is a translation, and the head-to-tail sum of the arrows representing them represents their composition. The head-to-tail summation method is called the parallelogram law of vector composition, but we have taken care not to use a parallelogram.

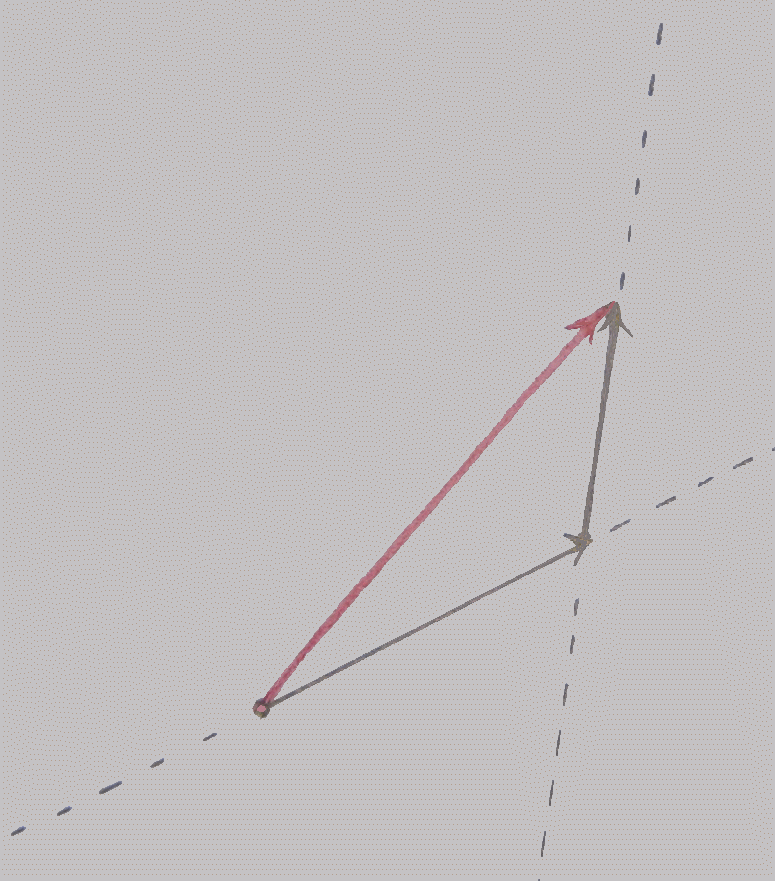
This suggests we might be able to find the result of two rotations in space, one after the other, by similarly adding their corresponding Turns on the Turn Sphere, head-to-tail, with sliding along a translation line changed to sliding along a great circle.

We said that a Turn or curved arrow represents the act of rotating about the center of the Turn Sphere in the direction of the arrow through an angle indicated by its length. The word “indicated” was intentionally vague. If taken to mean that the angle of rotation equals the length of the curved arrow, understood as a radian measure, then such a construction in general fails to give the correct answer. (It is correct only when the two arrows lie on the same great circle.) Consider an extreme example. Suppose we make two rotations each through 180° – a flip – about two perpendicular axes one after the other. A moment’s thought shows that the end result is the same as a flip about the axis perpendicular to the given axes. Yet the two curved arrows corresponding to the flips would be great-semicircles – if the arc length were the angle of rotation – and then their sum per the head-to-tail construction would be a curved arrow of zero length, a null Turn, that is, no rotation at all – which is about as wrong as possible.

However a simple modification or reinterpretation of our definition of a curved arrow / Turn will exactly compensate for the curvature of the sphere, to wit: make its arc length (in radians) exactly half the rotation angle. When we come to follow an arrow’s instructions, we double its numerical length to obtain how much to rotate. But when adding them we use them as they are, with the half angle. This modification will make the head-to-tail construction work in every situation. This amazing and little known theorem is due to Lawrence C. Biedenharn and James D. Louck, and can be found in “The Theory of Turns Adapted from Hamilton” which is chapter 4 of their Angular Momentum in Quantum Physics (1985), a volume of Encyclopedia of Mathematics and its Applications edited by G.-C. Rota.

Applied to our example of the two flips, the given curved arrows are now each 90° (π/2 radians) and adding them head-to-tail yields an arrow of 90° perpendicular to the given arrows – the correct result.

The theorem can be proven using the idea of reflection and two lemmas of solid geometry.

A reflection, like a rotation, takes objects in space to objects in space. It is determined by one plane and defined as follows. Given a plane, the reflection of a point is the point on the other side of the plane directly opposite, that is, the line between the given point and its reflection is perpendicular to the plane, and the two points are the same distance from it. A reflection changes an object into its mirror image; points on the plane remain where they are.

Lemma #1  Given two planes  A  and  B,  intersecting in the line  L,  the result of reflecting first through  A  and then through  B  is the same as rotating about  L  in the direction  A  to  B,  through twice the dihedral angle between them.

In other words, given two intersecting planes, if we first reflect objects in space “through” one plane and then the other, the resulting position of the objects will be the same as if they had been rotated about the line common to the planes, the angle of rotation being exactly twice the dihedral angle between them in the direction from the plane used first to the one used second.

This lemma, though about solid geometry, in essence is about plane geometry. Given an arbitrary point to be moved by the rotation, view the two reflecting planes end on, or what amounts to the same thing, consider the plane slice perpendicular to their intersection and through the given point. In that slice we have two intersecting lines – the angle between them is the dihedral angle – and the arbitrary point. The lemma says that reflecting that point through one line and then the other in effect rotates the point by twice the angle between the lines.

The end view of two planes, labeled first and second, intersecting at  30°.  Three points in various positions, each labeled  0,  are reflected in the first plane to points labeled  1,  and then these are reflected in the second plane to points labeled  2.  In each case he final point is the starting point rotated  60°.

The proof is based on the fact that the mirror image created by a reflection is undistorted; reflecting is a rigid transformation. The mirror image is, in every respect except “handedness” and position, just like the original. In consequence, if you expand a vector, its reflection – its mirror image – expands by the same amount. And if you add two vectors, their reflections add likewise, that is, the reflection of “their sum on the original side” is the sum of their reflections on the other side. These two properties can be written algebraically (for the moment, instead of using juxtaposition for multiplication we use a dot):
      mirror (c·V)       =  c·mirror (V)
      mirror (V + W)  =  mirror (V)  +  mirror (W)
An operation having these two properties is called a linear transformation. (This, by the way, is a more general concept than a rigid transformation; there are linear transformations that are not rigid.)

Thus the effect of reflecting any position vector (x,y) can be determined by its effect on just two: (1,0) and (0,1).  First decompose the vector like this (using juxtaposition for multiplication):
      (x, y)   =   x (1, 0)  +  y (0, 1)
Then use the observation above:
      mirror (x, y)   =   x mirror (1, 0)  +  y mirror (0, 1)

We assume the reader knows the formula for rotating a point about the origin:
      x’  =      x cos α +  y sin α
      y’  =  – x sin α  +  y cos α
(x’, y’)  is   (x, y)  rotated about  (0, 0)  by the angle  α.

Now suppose we are given two lines through the origin that define the first and second reflections. Choose an  x, y  coordinate system so that the intersection of the lines is the origin and the first line is the  x-axis.  Let   θ  be the angle from the first line (the  x-axis)  to the second line. Let  (x0, y0)  be a given point. Then the coordinates of its reflection in the first line are
      x1  =      x0
      y1  =  – y0
Where does reflecting in the second line take the point  (x1, y1) ?  This is where linear algebra can help. All we need to compute is the action on the two position vectors  (1, 0)  and  (0, 1).  Call the operation of reflecting in the second line, Ref. Per the diagram below, it in effect rotates the vector  (1, 0)  by  2θ,
      Ref  (1, 0)  =  (cos 2θ, – sin 2θ)


And it in effect rotates the vector  (0, 1)  by  2θ – π (which is in the opposite direction),
      Ref  (0, 1)  =  ( sin (2θ – π),  – cos (2θ – π) )
                        =  ( – sin 2θ,  – cos 2θ )


The result after the first reflection can be written as a linear combination of the basis vectors:
      (x1, y1)   =   x1 (1, 0)  +  y1 (0, 1)

Let  (x2, y2)  be the result after the second reflection, that is, of reflecting  (x1, y1)  in the second line:
      (x2, y2)   =   Ref (x1, y1)
Then because reflecting is a linear transformation as explained at the outset:
                   =   x1 Ref (1, 0)  +  y1 Ref (0, 1)

Plugging in the earlier expressions we obtained for  x1  and  y1  in terms of  x0  and  y0,  and then for the two  Ref’s  in terms of  θ:
      (x2, y2)   =   x0 Ref (1, 0)  –  y0 Ref (0, 1)
                   =   x0 (cos 2θ, – sin 2θ)  –  y0 ( – sin 2θ,  – cos 2θ )

Thus
      x2  =      x0 cos 2θ  +  y0 sin 2θ
      y2  =  – x0 sin 2θ  +  y0 cos 2θ
which is the given general point rotated by twice the dihedral angle, as we sought to prove.

Lemma #2  Given a line  L  and a plane containing it, and a second line  M  intersecting  L,  the plane can be rotated about  L  so it contains  M.

This is obvious; rotate the plane to the plane determined by the intersecting lines.
       

Thus given two intersecting lines each with a plane through it, the planes can be rotated about their respective lines so that they coincide. (The coincidence occurs at the plane determined by the intersecting lines.)
       

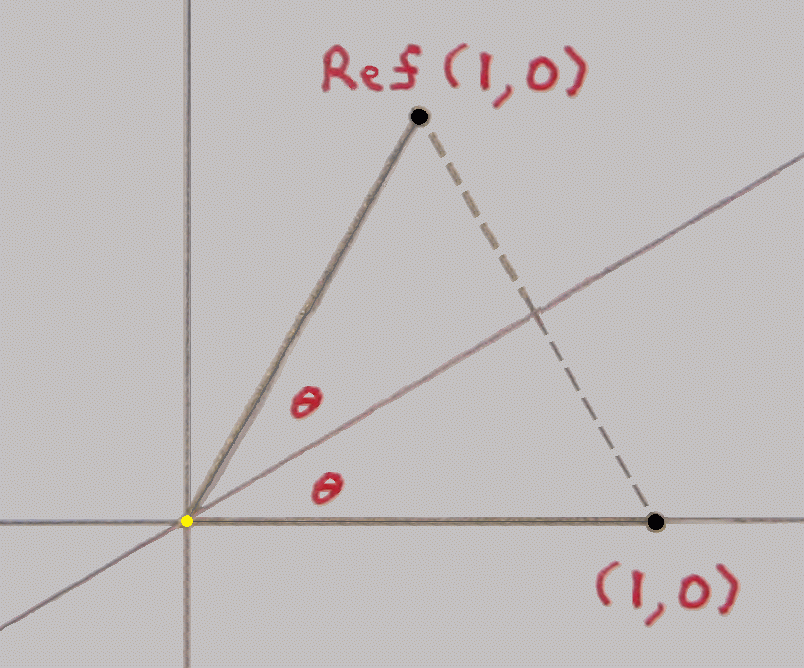
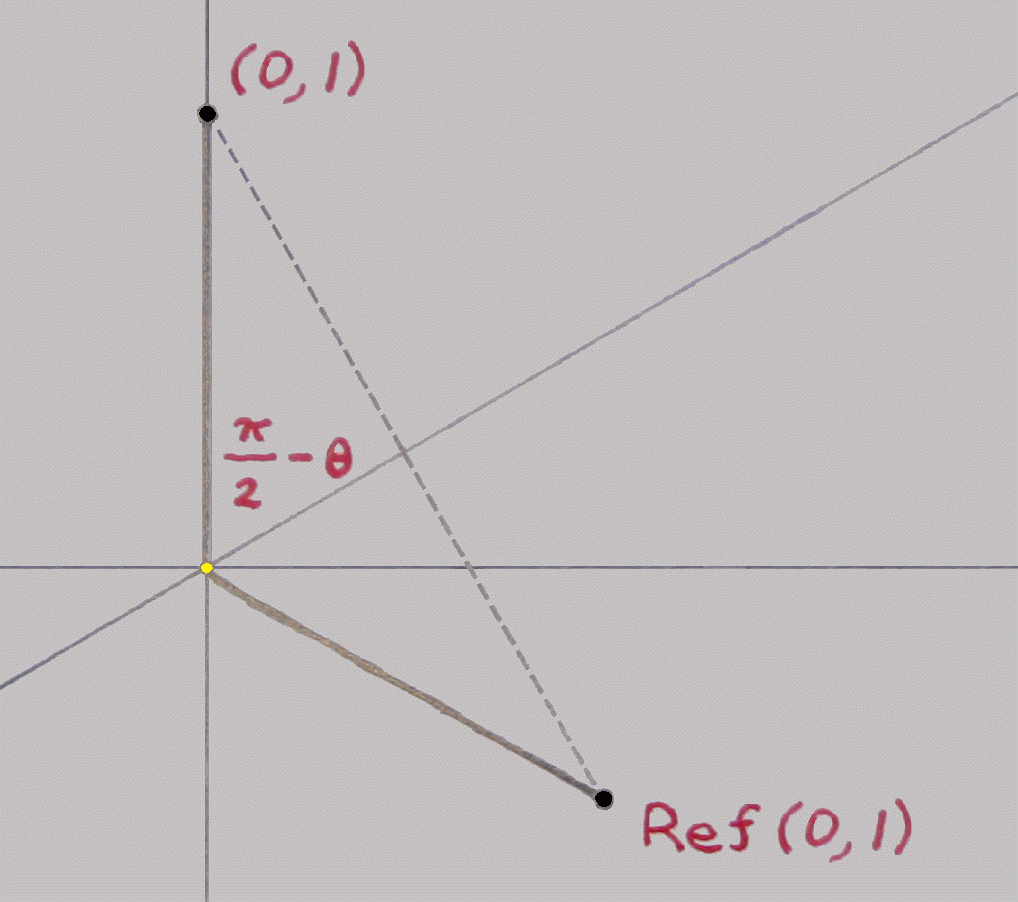
Now we are in position to prove the head-to-tail construction for composing rotations.

By Lemma #1 a rotation is equivalent to two reflections about an ordered pair of planes through the rotation axis, where the angle between the planes is exactly half the angle of rotation. We say that the ordered pair of planes represents the rotation.

Call such an ordered pair a paddelrad (German for “paddlewheel”) and each plane a paddel.


We need keep in mind only a rectangle of each plane of the paddelrad, two units wide (extended on each side of its axis by 1 unit) and of indeterminate length.

Because of Lemma #1, we can rotate a paddelrad about its axis by any amount and it will continue to represent the same rotation.

A paddelrad is equivalent to a curved arrow, with the first plane corresponding to the tail and the second to the head,


and the double reflection is equivalent to the rotation that the curved arrow indicates.

Euler’s theorem says that given two orientations there exists a rotation taking one to the other. Thus the change in orientation after two rotations is the same as that made by a single rotation. Paddelrads enable us to find that single rotation, as follows.

Consider two rotations (as usual about the same point) and let  A  and  B  be two paddelrads representing them per Lemma #1. Call their ordered planes  Atail Ahead  and  Btail Bhead  respectively, taking the names from the corresponding curved arrow. Consider the plane common to the axis of  A  and the axis of  B  and call it  P.  By Lemma #2, if we choose a paddel from  A  and one from  B,  their respective paddelrads can be rotated so that the chosen paddels coincide, specifically in the plane determined by the paddelrads’ axes,  P.  So rotate  A  on its axis so that  Ahead  lies on  P  and rotate  B  on its axis so that  Btail  lies on  P  as well.  Thus the four planes
      Atail Ahead Btail Bhead
become
      Atail P P Bhead
Now imagine these reflections being done in their given order. The two reflections through plane  P  in the middle cancel, and we are left with the single paddelrad
      Atail Bhead

Tom Verhoeff puts it this way in “Composing Rotations via Hamilton Turns” (after some abridgement and minor copyediting):


A Turn is a directed arc on a great circle of the unit sphere. Turns can be added like vectors, by sliding them along their great circle to place them head-to-tail. A rotation operation corresponds to a Turn that spans one-half of the rotation angle on the great circle perpendicular to the rotation axis.

A rotation is equivalent to the composition of two reflections in planes that intersect the rotation axis, with a dihedral angle equal to one-half of the rotation angle. This pair of reflection planes can be rotated freely about the rotation axis as long as the dihedral angle stays the same. We choose the middle two reflection planes to pass through both rotation axes, that is, the second reflection plane of the first rotation and the first reflection plane of the second rotation. This way, when composing the two rotations, the shared reflection in the middle cancels. Thus, we are left with an operation defined as two successive reflections, which is again a rotation. The composite rotation’s axis is the intersection of those outer two reflection planes, and the composite rotation’s angle is twice the dihedral angle of those planes.

The way of adding paddelrads in the proof is identical to the head-to-tail way of adding the associated curved arrows.

The proof shows that given two rotations one followed by the other, there exists a single rotation that has the same effect, which is a special case of Euler’s theorem.

When defining the curved arrow, only a rotation angle factor of one half will make head-to-tail addition work. The fact that in all cases that particular factor exactly compensates for the curvature of the sphere is what is so amazing.

Unlike with translations in the plane, the head-to-tail method of adding works only with two Turns at a time. The restriction on sliding a curved arrow only along its great circle prevents, in general, “daisy chaining,” the construction.  Codman’s Paradox provides an example of three Turns that cannot be slid head-to-tail simultaneously. Most any three Turns would do for such an example but these particular three are easy to compose and the result is the basis of a good parlor trick.

Ernest Amory Codman, a Boston surgeon (and very interesting man, look him up), described the following in a medical article of 1934 about the muscles of the shoulder:

Start with your right arm hanging by your side with the thumb of the hand pointing forward. With your shoulder as the pivot, lift your arm sideways straight out so it points to the right. Then swing your arm forward horizontally so it points ahead. Finally, swing your arm down to your side where it started. But its not quite where it started. Your thumb is now pointing toward you, that is, to the left instead of forward as at the start. The end result is that your arm rotated 90° within itself.

The three rotations about the shoulder were 90° each, around three perpendicular axes: the first about the horizontal backward axis, the second about the vertical axis, the third about the horizontal leftward axis. That resulted in a 90° rotation about the vertical axis – a rotation about the long axis of your arm despite your never seeming to have done it.

Here are three representative curved arrows for the three rotations.


Try as you might to slide the arrows along their great circles so that all three are head-to-tail simultaneously,  A to B to C,  you won’t be able to do it. The sum must be done in pairs.  Slide  A  and  B  to get  A + B,  then slide that arrow and  C  to get  (A + B) + C.

     

 Or slide  B  and  C,  then slide  A  and that resulting arrow to get  A + (B + C).  Either way yields the same result. (That rotation is an associative operation is proven using Turns in the Biedenharn & Louck reference above. They prove it algebraically in section 3. They claim to prove it geometrically in section 2, however that proof is flawed: it applies only when the three curved arrows can be slid head-to-tail simultaneously.)

Rotation is not a commutative operation. Codman’s three rotations can be used as an example. As before, start with your right arm hanging by your side, thumb pointing forward. Then do the three 90° rotations of the arm in reverse order: up, right, down  (C + B + A).  Your thumb ends, instead of pointing inward, pointing outward.

-oOo-

Lemma #1 applied to reflections in two planes. A similar theorem holds applied to flips about two lines, a flip being a rotation of 180° (π radians):

Lemma #3  Given two lines  L  and  M,  intersecting at the point  P,  the result of flipping first about  L  and then about  M  is the same as rotating about their common perpendicular line through  P  in the direction  L  to  M,  through twice the angle between them.

If this statement is true then rotating the two lines  L  and  M  about their common perpendicular line (keeping the angle between them fixed) has no effect on the resultant rotation. We call the two lines a propeller, analogous to the paddelrad of Lemma #1.  The plane of a propeller is perpendicular to the line of the corresponding paddelrad.

Proving Lemma #3 directly is not as easy as proving Lemma #1 because the space case does not revert to the plane case. It can be proved directly but to save time and effort we use Lemma #1 to prove it, as follows. Observe that a flip about a line restricted to any plane through that line is equivalent to a reflection. Given a propeller, consider its plane, that is, the plane determined by the two lines of the propeller. The two flips each affect that one plane the same as a reflection, consequently their composition rotates the plane as in Lemma #1. The composition of the two flips for all of space is a rigid transformation, thus it must rotate all of space likewise.

Lemma #2, used in the paddelrad proof, showed that given two intersecting lines each with a plane through it, the planes can be rotated about their respective lines so that they coincide. The analogue we need for flips is:

Lemma #4  Given two intersecting planes each containing a line through a common point, the lines can be rotated in their respective planes about the point so that they coincide.

This is obvious; rotate the lines to the intersection of the two planes.

We can again prove the head-to-tail construction for composing rotations only using propellers instead of paddelrads. The proof goes just as before except that the planes of paddelrads are changed to the lines of propellers.

*  See The Dirac String Trick.