Antitwister
How a Spinning Object
Can Remain Connected to
a Stationary One
Is it possible to connect a spinning object to a stationary one without a sliding joint? What else could prevent the connection from twisting, and eventually breaking apart?
Imagine a box with a ball in the middle. Elastic ropes tether the ball to the sides of the box. The ropes are solidly anchored at their ends, there are no sliding joints.
The ball begins to turn, carrying along the rope-ends attached to its surface.
The program Antitwister shows movies of the ball spinning any number times without the ropes breaking. It can also show the ball spinning while attached to the stationary enclosure by an elastic web that completely encircles the ball.
|
| 
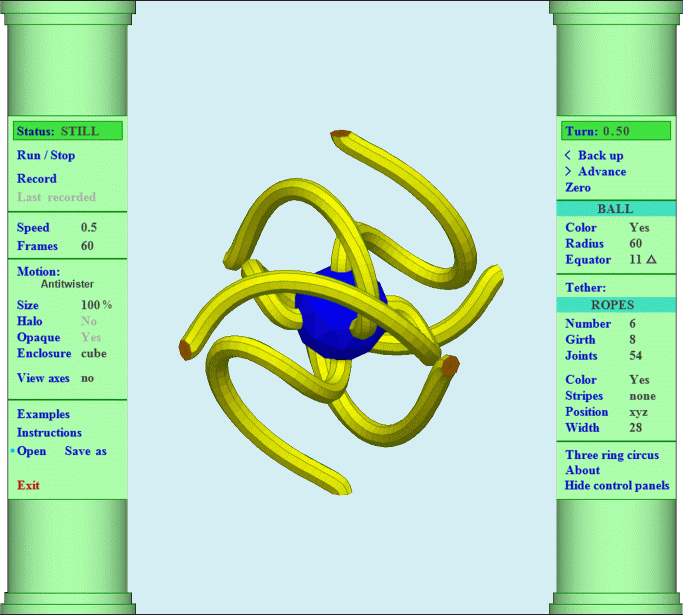
Some of the Motions the Program Can Show
Direct AntitwisterThe elastic never wraps around or twists beyond 360°.The elastic is straight and untwisted every two turns of the ball. | Adams AntitwisterHere the elastic is never straight and untwisted, its twist is always 180°.A pole rope moves in an especially simple way: it bends but never twists, it keeps its shape, and remains in a vertical plane. This plane rotates at exactly half the speed of the ball. | Dirac String TrickFirst the ball turns twice around, the elastic passively following. Then the ball stops, and remains stationary while the elastic moves to untwist itself. | Rotation of a RotationThe ball remains stationary. A 360° twist of the elastic in one direction turns over to a 360° twist in the other direction, and back again. The rotation of a rotation. | Dirac FlipFirst the ball turns once around, the elastic passively following, and stops. Then the elastic moves to reverse the twist as in the preceding motion. The ball then turns once more, the elastic passively following, and the twist is undone. | Spinning WheelTwister rather than Antitwister. The elastic twists ceaselessly as the ball remains stationary. (The motion, unlike that of the other motions, is not periodic.)A pole rope moves like the yarn in a spinning wheel’s flyer mechanism, which guides the yarn in a way to make it twist as it’s wound on the bobbin. |
CommentsI set up and ran Antitwister. I have to tell you that I am truly stunned and amazed. The continuous web images are especially intriguing. I had never seen the Adams machine, where the ball spins at exactly twice the rate of the orbiting rope. | | Antitwister is a cool program and it’s great fun modifying all the settings to see what happens and mesmerizing to watch it deal with any variable. |
Thank you for sending me your fascinating program. I never tried anything like it and I am delighted that I can do it.
Do you have something more theoretical to explain the background ? — László Tisza · · · Yes, see The Dirac String Trick.See also the U.S. patent for a mechanism invented by Dale A. Adams. |
|
(upgraded 1 December 2021)Program Download Page
| |